第一部 宇宙と量子と人間の心
第三章 心の神秘
意識はコンピュータに乗せられない
・意識というものは科学的に説明すべき問題である。
・図3-4は物質的世界と精神的世界をまとめたものである。
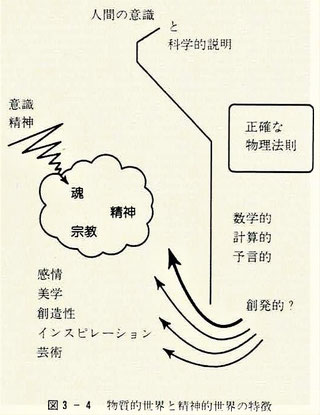
画像出展:「心は量子で語れるか」
『右側には“物質的世界”の様子が示されている―第一、第二で論じたように、物質的世界は、正確で数学的な物理法則によって支配されていると考えられる。左側には“精神的世界”に属する意識や、“魂”や“精神”や“宗教”などの言葉が並んでいる。』
微小管は八面六臂
・微小管はシナプス強度[シナプスにおける情報伝達率]の決定に関係していると思われる。
・微小管がシナプス強度に影響を与える方法の一つは、樹状突起棘の性質に影響を与えることであると思われる。これは棘内部のアクチン(筋肉収縮のメカニズムを司る不可欠な構成要素)に変質が起こることによって引き起こされる。樹状突起棘に隣接する微小管は、このアクチンに強く影響を与え、ひいてはシナプス結合の形またはその誘電特性に影響を及ぼす。
・『微小管がシナプス強度に影響を与える方法は、このほか少なくとも二通りある。信号を、あるニューロンから次のニューロンに伝える神経伝達物質の運搬に、確かに微小管は関与している。神経伝達物質を軸索や樹状突起に沿って運ぶのが微小管であり、その働きは、軸索の先端や樹状突起の中の化学物質の濃度に影響を与えるだろう。そして、これがシナプス強度に影響を及ぼすことになろう。さらに微小管は、ニューロンの成長と退化に影響を与え、その結果、ニューロンを連結してできたネットワークそのものを変えてしまうだろう。』
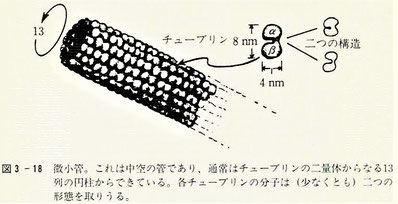
・『微小管とは何か? その一つを図3-18に描いた。それは“チューブリン”と呼ばれる、蛋白質から成る小さな管である。それはいろいろな点で興味深い。チューブリンは、(少なくとも)二つの異なる状態、または構造をもっていて、一方の構造から他方の構造へと変化できるようである。一見してわかるように、それはメッセージを管に沿って送ることができる。
事実、スチュアート・ハメロフ[米国の麻酔科医。ロジャー・ペンローズとの意識に関する共同研究で有名]と彼の同僚は、管に沿って信号を送る方法について、興味深い考え方を示している。ハメロフによると、たぶん微小管は“セル・オートマトン”[空間に格子状に敷き詰められた多数のセルが、近隣のセルと相互作用をする中で自らの状態を時間的に変化させていく「自動機械(オートマトン)」である。計算可能性理論、数学、物理学、複雑適応系、数理生物学、微小構造モデリングなどの研究で利用される]のように振る舞い、その管に沿って複雑な信号を伝達するのだという。チューブリンの二つの異なる構造が、デジタル・コンピュータの0と1を表現していると考えてみよう。すると1個の微小管が、それ自身でコンピュータのように振る舞うことができるから、ニューロンがどんなことを行っているかを考察する際には、この点を考慮しなければならない。各ニューロンは単にスイッチのような働きをするのではなく、非常に多くの微小管をもっていて、それぞれの微小管は極めて複雑なことをやってのけるのである。』
“意識”の理解に最も必要なこと
・『ここから、私自身の考えに入ろう。以上の過程を理解する上で、量子力学は欠かせないものかもしれない。微小管で私が最も興味をおぼえることの一つは、それらが“管”だということである。管であるがゆえに、管の内部で起こっていることを周囲のランダムな動きから隔離できる可能性が高まってくるのである。
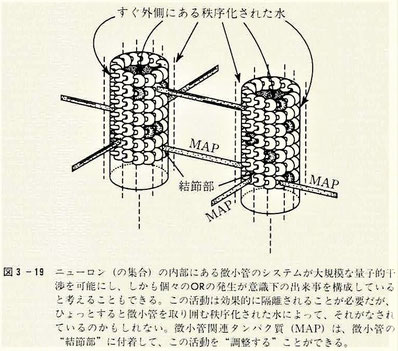
第二章で私はOR物理学という新しい形式が必要だと主張した。そしてOR物理学が適切であるならば、周囲から十分に隔離されて、量子的に重ね合わされた質量移動が可能になるに違いない。管内部では、何か超伝導体[電気抵抗ゼロの物質]のような、ある種の大規模な量子的干渉[波動関数の重ね合わせの結果起こる干渉現象]が生じているのだろう。この活動が(ハメロフ型の)チューブリン構造と結びつき始めたときにのみ、おそらく顕著な質量移動を伴うはずだ。ここでは“セル・オートマトン”の振る舞い自体が、量子的重ね合わせの影響を受けるかもしれない。起こりうる状況を図3-19に描いておいた。
この図の一部で、おそらくあるタイプの干渉性量子的振動が、管内部で生じているに違いない。この量子的振動は脳の広範な領域にまで及ぶ必要があろう。
かなり以前にハーバート・フレーリッヒが、一般的なタイプの量子的振動に関して、いくつかの提案を行った。それによって、生物学の体系の中で、この性質をもつ対象の存在が、いくぶん現実性を帯びてきた。微小管は、その内部で大規模な量子的干渉が生じている構造と考えて差し支えないと思われる。』
・『私には、意識というものが何か大域的なものだと思われる。したがって意識の原因となるどんな物理過程も、本質的に大域的な性質をもっているに違いない。量子的干渉は確かにこの点での要求を満たしている。そのような大規模な量子的干渉が可能であるためには高度な隔離が必要とされ、微小管の壁によって、それが実現されているのかもしれない。しかしチューブリンの構造が関与するとなると、さらに多くのことが必要となる。
こうして要求される周囲からの隔離は、微小管のすぐ外側にある“秩序化された水”によってなされるだろう。(生きた細胞には存在することが知られている) 秩序化された水は、管の内部で起こる量子的干渉性振動の重要な構成要素でもあると思われる。このことはいささか難しい要求かもしれないが、以上のことがどれも事実だということは、たぶん全くの不合理というわけではないだろう。
微小管内部での量子的振動は、何らかの方法で微小管の活動、すなわちハメロフが言うところのセル・オートマトンの活動と結びつける必要があるだろうが、ここでは彼の考え方と量子力学とを結びつけなければならない。すなわち現段階では、通常の意味での計算活動だけではなく、こうしたさまざまな活動の重ね合わせに関連する量子計算も考慮しなければならない。
もし以上の話がすべてだとしたら、まだ私たちは量子レベルにとどまっていることになる。ある時点で、おそらく量子状態は環境と絡み合ってくるだろう。そのとき私たちは、量子力学における通常のRという手順に従って、一見したところランダムな方法で古典レベルへ飛び上がることになる。だが純粋な計算不可能の登場を期待するならば、これでは全く不十分である。そのためには、ORの計算不可能な側面が現れてこなければならないし、それには高度な隔離が要求される。
かくして、新たなOR物理学が重要な役割を演じるのに十分な隔離を行う何かが、脳の内部に存在しなければならない。つまり私たち〔の脳〕に必要なのは、重ね合わされた微小管による計算が一旦開始されるや、その計算が十分に隔離されて、その結果、新しい物理学が本当にその役割を果たすようになることである。
というわけで、私が考えている状況は次のようになる。しばらくの間この量子計算が進行し、十分に長い間(たぶん一秒くらいのオーダーで)、その計算は他の要素から隔離され続ける。そうすると、私が話した種類の基準が通常の量子的手順を引き継いで、非計算的な構成要素が登場し、標準的な量子論とは本質的に異なる何かが得られるのである。
もちろん以上の考え方の至る所に、かなり推測が入っている。だがそれらは、意識と生物物理学的な過程との関係をかなりはっきりと定量的に描いており、私たちに何かしら本物の展望を与えている。少なくとも私たちは、OR作用が関与するためには、どのくらいのニューロンが必要かを計算できる。
その計算に必要なものは、第二章の終わりにかけて私が述べた時間スケールTの、およその見積もりである。つまり、意識上の出来事がORの出現と関係していると仮定するなら、Tをいくつと見積もるのか? 意識はどのくらいの時間を要するのか? これらの問題に関連した二つのタイプの実験があって、そのいずれにも、リベットと彼の同僚がかかわっている。二つの実験のうち一方は自由意志または能動的意識を、もう一方は、感覚または受動的意識を扱っている。』

画像出展:「心は量子で語れるか」
客観的収縮=OR
『将来、物理学が成し遂げねばならないと思うことを示すため、図2-17には修整が施されている。Rという文字で表現した手続きは、まだ私たちが見つけていない何かを近似したものである。その未発見の何かとは、私がORと呼ぶものであり、“客観的収縮(Objective Reduction)”を表してる。
ORは客観的事実である― 一方、“または”他方が客観的に起こる ―今なお私たちには欠落している理論である。ORというのは、うまい頭文字になっている。というのもORは“または”をも表しており、それは実際、一方“もしくは”(OR)他方のどちらかが起こるからである。』
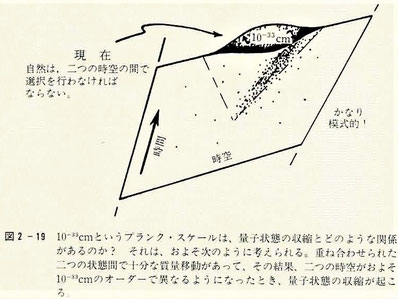
画像出展:「心は量子で語れるか」
自然が審判を下すための時間
『プランク長の10⁻33センチメートルは、量子状態の収縮とどんな関係があるのだろうか? 図2-19に、分岐しようとしている時空をかなり模式図的に示した。
ここで、二つの時空(一方は生きた猫を、他方は死んだ猫を表すことができる)が一つの重ね合わせに至る状態があって、この二つの時空は何とかして重ね合わせられる必要があるとしよう。このとき、次のような疑問が生じる。
「互いに法則を変えるべきだと思えるほど、二つの時空が十分に異なるようになるのはいつか?」
ある適切な意味で、二つの時空の差がおよそプランク長のオーダーに等しくなるとき、私たちはそのような状況に遭遇するだろう。二つの時空の幾何学がそれくらいの違いを見せ始めるとき、そのときこそ、私たちは法則が変わることを心配しなくてはならないだろう。なお、強調しておくが、私たちが扱っているのは時空であり、単なる空間ではない。
“プランク・スケールの時空分離”については、小さな空間的分離がより長い時間に対応し、より大きな空間的分離がより短い時間に対応する。ここで必要なのは、どんな場合に二つの時空が有意に異なるかを見積もるための評価基準である。
そこから、二つの時空の間で自然が選択を行う際の“時間スケール”が導かれるだろう。こうして自然は、私たちが未だ理解していない何らかの法則に従って、どちらか一方の時空を選択するのである。
この選択を行うのに、自然はどのくらいの時間を要するのか? アインシュタインの理論に対するニュートン的近似が十分であって、かつ、量子論重ね合わせ(二つの複素振幅の大きさは大体等しい)に従う二つの重力場が明らかに異なるとき、その時間スケールを設計することができる。私が示そうとする答えは、次のようになる。まず猫を球体で置き換えてみる。
では、その球体はどれくらいの大きさで、どこまで動かなければならないのか? また状態ベクトルの崩壊が生じるための時間スケールはどれくらいなのか(図2-20)?
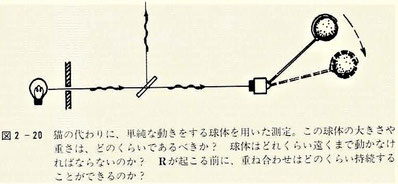
画像出展:「心は量子で語れるか」
私は、一つの状態ともう一つの重ね合わせを、不安定な状態―それは崩壊しかかっている素粒子やウラン原子核などに少し似ている―と見なしたい。素粒子などは崩壊すると別のものになるが、その崩壊と結びついた一定の時間スケールが存在する。状態の重ね合わせが不安定だというのは一つの仮説だが、この不安定性は、私たちが理解していない物理学の存在を暗示しているはずである。
崩壊の時間スケールを算出するため、ある状態の球体を、(その球体の)別の状態の重力場から移動させるために必要なエネルギーEを考えてみよう。プランク定数を2πで割ったℏ[換算プランク定数またはディラック定数]を重力エネルギーEで割ると、この状態での崩壊に対する時間スケールTとなるはずである。
T=ℏ/E
この一般的な推論に従う多くの理論がある。一般的な重力理論は、細かな点では違いがあるものの、どれもこれと何かしら同じ趣き〔似たような関係〕を備えている。』
“微小管”について
まずは「人体の正常構造と機能」という本に出ていた3つの図をご紹介します。
●微小管は太さ約24㎚の中空の管であり、チューブリンという蛋白質からできている。
●線毛や鞭毛の動きは微小管が行っている。
●神経の軸索突起などの大きな細胞突起を支持する。
●細胞分裂の際に、染色体を両極に引っぱる紡錘糸は微小管からできている。

画像出展:「人体の正常構造と機能」
■線毛の芯は“9+2配列”の微小管でできている
『線毛の中央部は直径0.25~0.3μmで、電子顕微鏡で観察すると、各線毛は細胞膜で囲まれ、その中に微小管とその付属蛋白からなる軸糸という構造が認められる。軸糸を構成する微小管は、チューブリンという球状蛋白が重合してできた管状の構造物で、外径25㎚、壁厚5㎚ほどある。軸糸の中心には1対の単一微小管からなる中心微小管があり、そのまわりを9対の二連微小管からなる周辺微小管が取り囲む。各周辺微小管の作る面は、線毛の接線面に対し5~10度傾いており、中心近くにあるものからA細管、B細管と呼ぶ。A細管と中心微小管とはスポークで連結される。またA細管から隣の周辺微小管のB細管に向かって、ダイニンというモーター蛋白でできた2本の腕突起(内腕と外腕)が伸びており、内腕はさらにネキシンの細い線維が結合している。これらは微小管の長軸方向に一定の間隔で並ぶ。線毛の先端側は微小管のプラス端にあたり、各微小管は自由な断端となって終わる。線毛の根元側は微小管のマイナス端にあたり、細胞質内まで伸びたところで周辺周辺微小管にさらにC細管が加わり、基底小体という三連微小管となる。この周辺には根小毛という線維束があり、線毛を細胞質に固定している。基底小体下にはミトコンドリアが豊富である。』
■線毛の屈曲運動は微小管の滑り合いによって起こる
『線毛の屈曲は、周辺微小管の滑り合いにより生じる。周辺微小管の腕突起を構成するダイニン蛋白はATPase活性を持ち、ATPの存在下で隣の微小管のB細管上をマイナス端へ向かって移動する。その結果、微小管どうしが滑り合い、線毛は屈曲する。滑り合いと屈曲運動の関係は、短柵状の紙を2枚に折って重ねて指で滑らせてみると納得がいくだろう。線毛内のスポークやその他の連結の役目をする構造物も、線毛運動の調節をしていると考えられている。』

画像出展:「人体の正常構造と機能」
■精子は長距離を移動するために無駄のない形をしている
『尾部[遊泳運動を担う]は長さ約60μmの鞭毛からなる。鞭毛の中心を軸糸と呼ばれる構造が全長にわたって走行している。軸糸は、2本の中心微小管とそれを取り巻く9対の周辺微小管で構成され、線毛にみられるのと同様の構造である。これらのチューブリンという蛋白質からなり、その滑り合いによって軸糸を屈曲させ、独特の三次元的波状運動をもたらす。軸糸の屈曲に要するエネルギーは、中間部の軸糸をらせん状に取り囲むように配列するミトコンドリア鞘で産生されるATPによって供給される。』

画像出展:「人体の正常構造と機能」
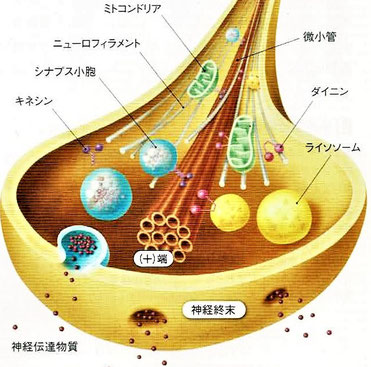
■軸索輸送によって必要な物質が供給される
『軸索内には蛋白合成を行う細胞内小器官がない。そのため、軸索の成長やシナプスの形成に必要な蛋白質や小器官は、細胞体で合成されたのち、軸索を通って輸送される。これを順行性軸索輸送という、逆に、神経終末で取り込まれた栄養因子や化学物質は、逆行性軸索輸送により細胞体へ輸送される。微小管がこれらの輸送のレールの役目を果たし、モーター蛋白のキネシンをはじめとするKIF蛋白は順行性の輸送に、ダイニンは逆行性の輸送に働く。
順行性輸送では、いろいろな物質が異なる速さで運ばれる。シナプス小胞は速い流れ(100~400㎜/day)で、ミトコンドリアは中間の流れ(60㎜/day)で、細胞骨格(アクチン、ニューロフィラメント、微小管)は遅い流れ(10㎜/day以下)で運ばれる。逆行性輸送では、100~200㎜/dayの速さでライソソームなどが運ばれる。
軸索内では、微小管はチューブリンの重合と脱重合の速度が速い分、つまり微小管の伸長している部分(プラス端)は絶えず遠位側にある。また、軸索にはタウ蛋白と呼ばれる微小管関連蛋白が特異的に分布しており、チューブリンの重合を促進し微小管の安定化に寄与している。』
続いて、「病気を治す飲水法」に出ていたもの(ブログは“飲水の重要性”)と、その時に見つけたサイトをご紹介します。

画像出展:「病気を治す飲水法」
『脳で生産された物質は、水に乗って、神経終末部の目標地点にたどり着き、情報の伝達に使われる。神経には、情報を梱包して流す「極微細管」と呼ばれる微細な水路が存在する。』
原文が確認できないので、“極微細管”が“微小管”のことであるのかは分からないのですが、図を見る限り、同一のものだと思われます。この図に興味をもったのは、「神経伝達に水路がある」ということに大変驚いたためです。
この時、この“水路”に関してネットで見つけたサイトが以下のものになります。残念ながら“水路”というものではなかったのですが、絵が似ていたことと、「細胞内輸送の解明にかける思い」という記事から関係があるように思いました。

画像出展:「UTokyo Focus」
『細胞は細胞液の入った風船のようなもので、その中に核やミトコンドリアなどの細胞小器官が漂っていると思われがちです。しかし、実際には、微小管というレールが整然と張り巡らされており、それに沿ってミトコンドリアや小胞(膜でできた袋)などの「荷物」が行き来しています。これを「細胞内輸送」といいます。レールの上で荷物を運んでいるのは、小さなモータータンパク質です。「モータータンパク質が人間のサイズだとしたら、直径5mの土管の上を、10トントラックをかついで、秒速100m以上の速さで走っていることになります」と語るのは、医学研究科の廣川信隆特任教授。神経細胞をモデルとして、細胞内輸送のメカニズム解明に取り組んできました。』
感想
「心や意識は脳が作り出すもの」。これは正確ではないかもしれませんが、深く関係しているのは間違いありません。
ストレスは脳にアタックをかけます。脳が疲労し、その疲労が身体におよぶと自律神経失調症が懸念されます。ちょっと強引ですが、「病は気から」ということわざの“気”は脳の疲労などによってもたらされた“ネガティブな意識”ということかもしれません。
一方、「ポジティブ・シンキング」、「瞑想法」などはネガティブなストレスとは異なり、心身にとって良いポジティブなものですが、こちらも脳(心や意識)と肉体のつながりを感じさせます。
以下の左図に書かれているように脳は“神経系”の中の“中枢神経系”とよばれています。これは脳が指令を出すためです。出された指令は“末梢神経系”によって然るべき組織や器官に届きます。“末梢神経系”には運動や感覚などの動物性機能を担う体性神経系(動物神経系)と、内臓や血管に分布して呼吸、消化、吸収、循環、分泌などの活動を不随意的に調節する自律神経系(植物神経系)があります。
なお、右側の図を見て頂くと、“神経系”は内臓を含め、体中をカバーしているのが分かります。
注)2つの図は「看護roo!」さまより拝借しました。
左図:“神経系はどんな構成になっている?”より
右図:“神経のしくみと働き|神経系の機能”より


左の図では“交感神経”も“副交感神経”も「遠心性」(脳⇒末梢)となっていますが、現在は次のような見解が正しいとされています。つまり、“自律神経”は「遠心性+求心性」(脳⇔末梢)ということです。
『求心性神経と遠心性神経:自律神経系(交感神経と副交感神経)は、かつては遠心性の線維のみからなるとされていたが、求心性線維も多く含まれていることがわかってきた。迷走神経(副交感神経)構成線維の約75%、内臓神経(交感神経)の50%は求心性線維とされている。 実験医学 2010年6月号 Vol.28 No.9』
“神経”は我々のような動物だけでなく、ゾウリムシのような単細胞生物にも存在します(「動くニューロン[神経細胞]」と呼ばれているそうです)。また、神経ということではありませんが、微生物とされるバクテリアの線毛にも微小管は存在しています。
以上のことから神経細胞の輸送のためのレールなど、微小管は地球上の多くの生物の中にあり、生命に深く関わっていると言えます。さらに、微小管は精子の尾部(鞭毛)にも存在しているので、種の保存という大事な仕事も任されています。
そして微小管はペンローズ先生がご指摘されているように“管”として内部と外部を分けることができるという大変興味深い特徴を有しています。マクロ(ニュートン力学)の世界とミクロ(量子力学)の世界を分けているのかも知れません。
ペンローズ先生は「心は量子で語れるか」の中で、“微小管”と“水”の関係についてもお話されていました。
『私には、意識というものが何か大域的なものだと思われる。したがって意識の原因となるどんな物理過程も、本質的に大域的な性質をもっているに違いない。量子的干渉は確かにこの点での要求を満たしている。そのような大規模な量子的干渉が可能であるためには高度な隔離が必要とされ、微小管の壁によって、それが実現されているのかもしれない。しかしチューブリンの構造が関与するとなると、さらに多くのことが必要となる。
こうして要求される周囲からの隔離は、微小管のすぐ外側にある“秩序化された水”によってなされるだろう(生きた細胞には存在することが知られている)。秩序化された水は、管の内部で起こる量子的干渉性振動の重要な構成要素でもあると思われる。』
この“水”は鍼灸師の私にとってとても興味深いものです。
人間の体は成人では60~65%が水で満たされています。また、東洋医学には“津液(シンエキ)”という考え方があります。津液とは人体を潤す全ての正常な水液とされています。この津液をあえて現代医学に当てはめて意識するときに、汗や涙、唾液や胃液、血漿、リンパ、漿液、脳脊髄液などを想像していました。今回の件で、その水の中には神経伝達に関わる水、微小管のすぐ外側にある“秩序化された水”があることを知りました。これは大きな発見です。私の“津液”のイメージにこの”秩序化された水”も加えたいと思います。
付記:ロジャー・ペンローズ先生は、2020年のノーベル物理学賞を受賞されました。

画像出展:「SankeiBiz」

画像出展:「WAKARA」
アインシュタイン以来の天才!?ノーベル物理学賞受賞ロジャー・ペンローズが生み出した現代宇宙観
『実は、ブラックホールが存在する可能性に気づいたのは、ペンローズが初めてではありません。天体物理学者カー・シュヴァルツシルトが、相対性理論の重要な方程式であるアインシュタイン方程式を解いてみたところ、ある特殊解が得られて、その結果特異点が存在することに気づきました。のちにブラックホール発見の重要なきっかけとなった特異点ですが、当時アインシュタイン自身はこの特異点について、「あくまで理論的な計算の結果出てきたもので、実在するものとは無関係である」と判断し、1939年の自身の論文でブラックホールの存在を明確に否定しているのです。
その説をアインシュタインが相対性理論を生み出した方法と同じ、計算によって覆して見せたのがペンローズでした。彼は相対性理論を拡張し、特異点、つまりブラックホールが相対性理論から自然に導かれる存在であることを証明しました。星の大きさに対して一定の重さになるとその星が崩壊し特異点を生じ、その特異点ではあらゆる物質、光でさえも一度入ると抜け出せない、ブラックホールになることを相対性理論から導いて見せたのです!彼が1965年に書いた画期的な論文は、相対性理論におけるアインシュタイン以来の前進とみなされています。』