なぜ、量子論という超難解なものに興味を持ったのかというと、それはブログ“がんと自然治癒力8”で勉強させていただいた、ブルース・リプトン先生の「思考のすごい力」という本に因ります。
この本の第四章は次の通りです。
第四章 量子物理学が生物学・医学を変える日は近い
量子物理学と縁なく過ごしてきたわたし
ニュートン力学では超常現象を解明できない
物質はエネルギーでできている
人間の生体内システムは重複的
製薬会社の駒となっている医師たち
電磁エネルギーが生体調整に深い影響を与える
代替医療の研究が進まないわけ
エネルギー波を治療に活用する
大袈裟ですが、私の背中を押したのは以下の4つです。また、キーワードは“エネルギー”であり、そして“量子論と東洋医学の類似性??”という期待のような思いを含んだ好奇心です。
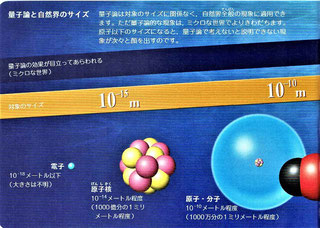
①『原子が宇宙で最も小さい粒子であるという概念は捨て去られた。一つの原子はさらに小さな粒子から構成されていることがわかった。これだけでも驚天動地の大発見だが、さらに、原子がX線や放射線など、さまざまな「奇妙なエネルギー」を放出していることが明らかになり、大騒ぎになった。』
②『ニュートン的で物質偏重主義である旧来の概念から抜け出せない研究者たちは、健康や病気にエネルギーの振動が果たす役割をまったく無視している。』
③『何千年も前、西洋の科学者が量子物理学の法則を発見するより遥か以前に、アジア人は健康と幸福に寄与する第一の要因として、エネルギーを尊んできた。』
④『東洋医学では、身体はエネルギーの経路(経絡)が複雑に列をなしたものと定義される。中国の鍼灸療法で用いられる人体の経絡図には、電気配線図にも似たエネルギーのネットワークが描かれている。中国医学の医師は、鍼などを用いて患者のエネルギー回路をテストするわけだが、これはまさに電気技師がプリント基板を「トラブルシュート」して電気的な「病変」を発見しようとするのと同じやり方だ。』
読んだ本は、「思考のすごい力」の中で紹介されていた2冊を含め、全部で4冊です。
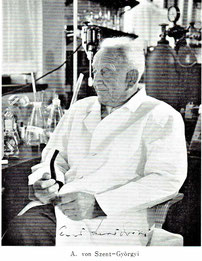
著書:「分子生物学入門」
著者:セント=ジェルジ・アルベルト
出版:廣川書店
発行:1964年9月
ジェルジ・アルベルト先生は、ビタミンCの発見などにより、1937年度ノーベル生理学医学賞を受賞されました。
写真は本書の中に掲載されているものです。また、この「分子生物学入門」の内容は極めて高度であり、タッチできるものではありませんでしたが、唯一、お伝えできる、お伝えしたいことは以下の文章の中の太字部分です。
『私の研究歴は組織学にはじまりましたが細胞形態学が与え得る生命についての知識に満足できず私は生理学に転じました。そこで生理学があまりにも複雑であることを見い出し私は薬理学の分野に転向いたしました。それは薬理学の対象の一つである薬物の性質が比較的に単純なものであると思われたからであります。しかしながら薬理学が決して単純なものでないことを知った私は次に細菌学の世界に踏み込んだのであります。ここでなおも細菌の複雑さを知らされた私は次第に分子レベルの問題に興味をひかれ化学や物理化学の研究をするようになったのであります。この経験を生かして私は筋肉の研究をはじめることを企てました。その後20年間にわたる研究の結果、筋肉の問題を理解するためには量子力学の法則に支配されている電子のレベルまで掘り下げる必要があるという結論に到達しました。』

監修:和田純夫
出版:ニュートンプレス
発行:2018年7月
※ブログ内の緑色『』は「13歳からの量子論のきほん」からの引用になります。
※上部に”常識が通じない! ミクロの世界の物理法則”とあります。
今回の“量子論1”は、自分自身の関心事に対して、できる限り分かりやすくまとめることを目標としました。一方、次回の“量子論2”では、H.R. パージェルの著書「量子の世界」を中心に全体像をつかむという点に重きを置きました。
相対性理論といえばアインシュタインですが、量子論といえば誰なのか? その答えは、ニールス・ボーアとその仲間達ということになります。
左の絵の中に、“シュレーディンガーの猫”と書かれたイラストが出ています。簡単にご説明すると、量子力学の基本となる方程式(“シュレーディンガー方程式”)を編み出したシュレーディンガーが、ボーア達が確立した“コペンハーゲン解釈”という考えに反旗を翻し、提示した宿題であり、“シュレーディンガーの猫”と命名されました。右の絵はその内容です。なお、この宿題は現在もクリアできず、“コペンハーゲン解釈”が完全なものに至っていない大きな理由の一つとなっています。
1.量子論と東洋医学
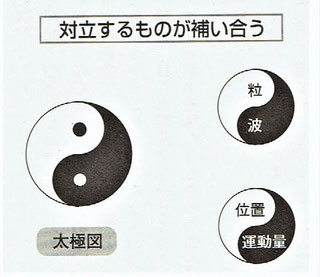
ボーアは量子論が明らかにした物質観・自然観の特徴を“相補性”という概念で説明していますが、ボーアはこの“相補性”を表すシンボルとして古代中国の「陰陽思想」を象徴する“太極図”を好んで用いたとのことです。このことは、「量子論を楽しむ本」の中に書かれていました。
『ボーアは相補性を表すシンボルとして古代中国の「陰陽思想」を象徴する太極図を好んで用いました。陰と陽という対立する「気」が絡み合い、相互作用をおこなうことで、すべての自然現象や人間活動が決まるとする陰陽思想は、まさに量子論の描く世界像と同じと言えます。ボーアは自分の紋章の一部に太極図を描いたほどでした。
量子論はこのように、中国思想などの東洋思想と相通じる部分を持つために、その観点から関心を持つ人も多くいます。東洋思想の柱に「一元論」があり、これは近代科学の根底にある「二元論」と対立する概念です。物と心、自然と人間などを分けて取り扱うのが二元論であり、これらを不可分なものとみなすのが一元論です。客観的事実を否定した量子論は、自然と観測者を分けて考える二元論的な世界観を退け、観測対象である自然と観測する私たちとを一つのセットとして考える、一元的な自然観を示すのです。』
東洋医学そのものではありませんが、ボーアがその大元になっている陰陽思想への関心が高かったという事実の発見は、驚きでもあり、うれしい気持ちになります。

写真はQingYang gong templeという寺院にある彫刻です。中央が太極図、まわりは十二支です。
画像出典:「ウキペディア」
2.量子論とは
1)アイザック・ニュートンと決定論

この画像は“山賀 進のWeb site”さまの“ニュートン略伝”から拝借しました。
量子論と対極にあるのは、アイザック・ニュートンの理論です。また、そのニュートン力学の考えをさらに発展させたのが、ピエール・ラプラスの「未来はきまっている」という考えです。まずは、量子論と比較する目的で「古典論」とされている、ニュートン力学と決定論について触れたいと思います。
『量子論が誕生する以前、あらゆる物体の運動は、「ニュートン力学」で説明できると考えられていました。ニュートン力学はイギリスの天才科学者アイザック・ニュートンが打ち立てた理論で、物体が力を受けてどのように運動するかを説明する理論といえます。
ボールの遠投を考えましょう。空気抵抗などは無視できるとします。ボールを投げた瞬間の速さと向き、高さが厳密にわかれば、地面に落ちる位置はニュートン力学によって厳密に計算できます。つまり「ボールの落下地点は、投げる瞬間に決まっている」といえるわけです。
サイコロの出る目が予測できないのは、サイコロを投げた瞬間の状態を厳密に知ることが困難だからです。投げた速さ、角度、高さなど、すべての条件が厳密にわかれば、出る目は計算できます。つまり、「サイコロの出る目も、投げる瞬間に決まっている」といえるでしょう。
フランスの科学者ピエール・ラプラスは、ニュートン力学の考えをさらに発展させて、次のように考えました。
「仮に、宇宙のすべての物質の現在の状態を厳密に知っている生物がいたら、その生物は宇宙の未来のすべてを完全に予言することができるだろう。つまり、未来は決まっていることになる」。この仮想的な生き物は、「ラプラスの魔物」と呼ばれています。
ラプラスのような考え方は、量子論が登場するまでは、物理学者の間で一般的だったようです。未来を予言することができないのは、人間の能力に限界があるためであって、実際には未来は決まっている。そう考えるわけです。
しかし量子論の登場によって、この考え方は正しくないことがわかりました。量子論によると、仮にラプラスの魔物が宇宙のすべての情報を知ることができたとしても、未来がどうなるかを予言することは原理的に不可能だからです。
たとえば電子は、運動方向を正確に決めると位置が不確かになり、位置を正確に決めると運動方向が不確かになります。電子の位置と運動方向を、同時に正確に決めることは不可能なのです。
このようにミクロの世界では、電子一つをとってみても、未来の予言は不可能です。つまり、未来はきまっていないようなのです!』
2)量子論が生まれた理由
『あらゆる物質は、「原子」からできていることがわかっています。19世紀末ごろになって、原子がかかわる現象を詳しく調べてみると、ミクロな世界は私たちが日常生活で目にする世界とはまったくちがうことがわかってきました。ミクロな物質は、私たちの常識では説明できない、摩訶不思議なふるまいをするのです。そこで、新しい理論が必要になりました。それが「量子論」です。量子論とは「非常に小さなミクロな世界で、物質を構成する粒子や光などがどのようにふるまうかを解き明かす理論」といえます。』
3)量子論と日常生活の関係
こちらの絵も「13歳からの量子論のきほん」からのものです。量子論はミクロの世界で顕著ですが、実はミクロの世界だけの話ではありません。
『量子論は、原子や電子といったとても小さいものがどのようにふるまうかを説明する、物理学の大理論です。現代の物理学は、一部の例外をのぞいて、すべて量子論という土台の上に築かれているといっても過言ではありません。量子論以前の物理学は、「古典論」とよばれます。原子より小さいようなミクロな世界は、古典論では説明がつかず、量子論という新しい理論が生まれたのです。
では量子論は、私たちが日常目にする世界(マクロな世界)とは、無関係なのでしょうか。実は量子論は、ミクロな世界であろうと、マクロは世界であろうと、自然界のすべてのサイズで適用できます。ただ、マクロな世界では、量子論の効果がほとんど見られなくなります。量子論が「ミクロな世界の物理法則」といわれるのは、量子論の効果が目立ってあらわれるのが、ミクロな世界だからなのです。
ただし、ミクロな世界もマクロな世界も、量子論だけですべてがこと足りるというわけではありません。たとえば、マクロな世界の物体の運動に量子論を適用すると、計算量が膨大になってしまいます。そこで実用上は、計算が楽な古典論が使われます。マクロな世界では、量子論による計算結果と古典論による計算結果が、ほとんど同じになるのです。
なおマクロな世界にも、量子論を使わないと説明できない現象はあります。「金属(導体)」「絶縁体」「半導体」の性質のちがいや、「超流動」や「超電導」といった現象です。
量子論であつかうミクロな世界の現象は、日常ではほとんど見ることができないので、量子論に慣れるのはむずかしいといえます。「人間が知覚できる世界は非常に特殊で限られている」という事実を、忘れないようにする必要があるでしょう。』
この「ミクロとマクロ」、「古典論と量子論」の関係性をつかむことは重要と考えますので、専門的ですが、以下に「量子の世界」の“第五章 不確定性と相補性”から一部を引用させて頂きます。
なお、ポイントは「例えば細菌サイズであっても、不確定さは10億分の1しかないため、ニュートン力学でも問題ない誤差であるが、原子サイズになると不確定さは100分の1と高くなるため、いよいよニュートン力学では難しくなってくる」というような内容です。
『いろいろな対象に対して、ハイゼンベルクの関係式がどの程度の意味をもつかのだいたいの感じをつかむためには、その対象のサイズと代表的な運動量を掛け合わせたものを、ブランク定数h―量子効果が重要となる目安―と比較してみるとよい。飛んでいるテニスボールについて言えば、量子論による不確定さはおよそ1000万×10億×10億×10億分の1(10のマイナス34乗)に過ぎないことがわかる。したがって、テニスボールは十分な高精度で古典物理学の決定論的法則に従っていると言ってよい。細菌でさえ、その効果はおよそ10億分の1(10のマイナス9乗)の程度で、量子世界を全く経験することはないのだ。だが結晶中の原子になると我々は量子世界の入口まで迫っていくことになり、不確定さが100分の1(10のマイナス2乗)になる。ついに原子の中を動き回る電子に至っては量子的不確定性が完全に支配的となり、我々は不確定性原理と量子力学を支配者とする正真正銘の量子世界に足を踏み入れることになるのだ。』
実は、今回「ハイゼンベルクの関係式」を調べていて、大きな修正が起きていたことを知り大変驚きました。それは以下の記事です。なお、この修正は上記の内容(物質の大きさと法則の関係性)に大きな影響を与えるものではないと思われます。
【クローズアップ科学】ノーベル賞「重力波」に陰の立役者 名大・小澤正直特任教授、物理学の定説覆す理論で貢献 2017.10.8 10:00
“~ 量子力学を象徴するとされてきたハイゼンベルクの不確定性原理を表す不等式の破れ(欠陥)を正した「小澤の不等式」でも世界的に知られている。ハイゼンベルクの不等式は「物体の位置を正確に測ろうとすると、測定によって起こる運動量の乱れが大きくなる」ことを表す。測定誤差がゼロだと、運動量が無限大になるので、そのような測定はできないと考えられてきた。これに対して、小澤氏が2003年に発表した不等式は、誤差ゼロの測定が可能であることを示す。量子の世界の「不確かさ」には測定に伴う誤差や運動量の乱れと、測定とは関係なく量子が本来的に持っている位置や運動量の「揺らぎ」がある。小澤氏は、2つの「不確かさ」がきちんと区別されないまま80年にわたり定着していたハイゼンベルクの不等式の間違いを正し、完全な式を提示した。 ~”
4)量子論の二つの重要事項
●「波と粒子の二面性」:“電子や光は、波と粒子の性質をあわせもつ”
●「状態の共存(重ね合わせ)」:“一つの電子は、箱の左右に同時に存在できる”
これについてはここでは触れません。その代わり、勇気づけてくれる一文をご紹介します。それは「量子の世界」の“第九章 波を作る”の冒頭(添書き)に書かれているものです。
『量子力学が本当に理解できている人はまずいないだろう、と言って私は間違っていないと思う。諸君はもしできるなら、「だが、どうしてそんなことがありうるのだろうか」と自分自身に問い続けるのはやめた方がよい。なぜならますます深みにはまって、袋小路をさまようのが落ちで、そこから出口を見つけて出てきた人はまだいないのだから。どうして量子力学ではそうなるのかは、誰もわかってはいないのだ。』
なお、この文章は、リチャード・フィリップス・ファインマンの言葉です。ファインマンは、経路積分という新しい量子化の手法を考案し、この成果により1965年にノーベル物理学賞を受賞された物理学者です。
5)“コペンハーゲン解釈”とは
現在、解決できない宿題(既出の“シュレーディンガーの猫”の件など)はあるものの、量子論の代表的な解釈は“コペンハーゲン解釈”と呼ばれているものです。以下はネット上にあった「知恵蔵」による解説です。
『コペンハーゲン解釈は、N.ボーアやW.ハイゼンベルクらの立場に沿うもので、正統派解釈とされる。この見方では、量子世界の物理状態は重ね合わさり、波を形づくっているが、観測された瞬間に波はしぼみ、1つの状態に落ち着く(波束の収縮)。どの状態が観測されるかは、波の振幅をもとに確率論的に予想できる。収縮の原因として、測定する側(環境)が測定される側に乱れを起こすことなどが考えられている。』
一方、「量子論を楽しむ本」の中の説明は以下の通りです。
『「波の収縮」と「確率解釈」を二本の柱として、私たちに見られる前の電子と見られた後の電子のようすを理解しようとするこの解釈方法を、コペンハーゲン解釈と呼びます。』
また、「13歳からの量子論のきほん」の説明は次のようなものです。
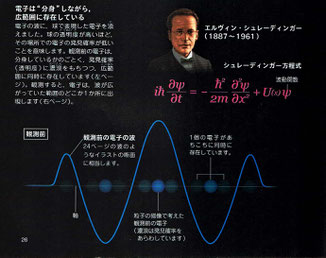
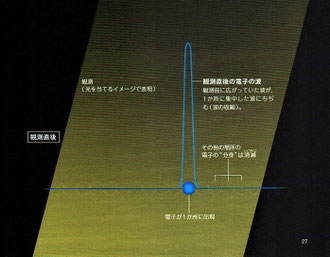
観測すると、電子の波が瞬時にちぢむ!? “とがった波”が、粒子のようにみえる
『一つの電子は「波と粒子の二面性」をもちます。この矛盾したような事実は、どう解釈したらよいのでしょうか。コペンハーゲンを中心に活躍したデンマークの物理学者のニールス・ボーア(1885~1962)らは、「コペンハーゲン解釈」とよばれる解釈を提案しました。
コペンハーゲン解釈によると、電子は観測していないときは、波の性質を保ちながら空間に広がっています。しかし、光を当てるなどして電子を観測すると、波が瞬時にちぢみ、1か所に集中した“とがった波”になります(波の収縮)。このような波が、粒子のように見えるというのです。
電子は、観測すると、観測前に波として広がっていた範囲内のどこかに出現します。しかしどこに出現するかは、確率的にしかわかりません。このような解釈をすれば、電子などの「波と粒子の二面性」を矛盾なく説明できると、ボーアらは考えたのです。』
電子は、“分身”しながら広範囲に存在している 電子の波を、発見確率をあらわす波と考える
『電子の波とは、いったいどんな意味をもつものなのでしょうか?
先にご紹介したように、観測前の電子は、波のように空間に広がっています。これをあえて粒子的な描像で考えると、「一つの電子が、漫画などにえがかれる分身の術をしている忍者のごとく、あちこちに同時に存在している」といったイメージになります。
電子が発見される確率は、電子の波の“山の頂上”または“谷の底”で最大になり、電子の波が軸と交わっているところでゼロになっています。このように電子の波を、電子の発見確率をあらわす波と考えるのが、量子論の標準的な解釈となっている「コペンハーゲン解釈」です。
電子の波を数学的にあらわしたものは、「波動関数」とよばれています。電子の波動関数が原子の中などで、どのような形をとるかを導くための量子論の基礎方程式を、「シュレーディンガー方程式」といいます。』
3.おさらい
この“おさらい”は、「量子論を楽しむ本」の中にある“ミクロの世界の物理法則が明らかになる”の内容です。量子論を理解する上で、量子論を古典派と推進派の両面から理解することが重要ではないかと考えました。
“ミクロの世界の物理法則が明らかになる”
『さて、3章(見ようとすると見えない波)でもさまざまな話をしてきました。最後は例によってこの章のポイントをおさらいしておきましょう。
①原子中の電子の軌道半径がとびとびの値に限られるというボーアの量子条件の根拠を示すために、ド・ブロイは電子を波であると考えて、その波長を求めた。
②シュレーディンガーは電子の波を表すシュレーディンガー方程式を導き、電子の「とびとび」のエネルギー状態などの説明に成功した。
③しかしシュレーディンガー方程式が示す波動関数ψ(プサイ)、すなわち電子の波(これは複素数の波である)の正体はわからなかった。
④ボルンは波動関数ψそのものが何を表すのかを考えずに、代わりにψの絶対値の二乗が、電子をその場所に発見する確率に比例することを見いだした(「波動関数の確率解釈」)。
⑤ボーアたちは、観測される前の電子はさまざまな位置にいる状態が「重ね合わせ」になっているが、私たちが電子を観測したとたんに「波の収縮」が起きて電子は一ヶ所で発見されると考えた(「コペンハーゲン解釈」)。
こうして1920年代に、原子中の電子が示す不思議な現象をきちんと説明できる理論を、私たちはついに手にすることになりました。そしてその結果わかったのは「電子などミクロの世界は、私たちが知っていた物理法則とはまったく違うルールに支配されていたのだ」ということです。
その新たなルールの第一は、シュレーディンガー方程式に代表される波動力学(量子力学)です。ミクロの世界の物質は、それを「波である」と考えることでふるまい(動きやエネルギー)などを求めることができるのです。
そしてもう一つのルールが「確率」です。私たちが電子を発見する場所は、サイコロを振って決められるかのように、確率的に決定されるというのです。』
このおさらい①~⑤を眺めると、古典派と推進派の違いは、波動関数の正体にこだわり歩を止めたアインシュタインやシュレーディンガーなどの古典派(決定論[ニュートン以来の物理学の大前提]を尊重)と、波動関数の正体を明らかにすることを先送りし、波動関数の存在を前提として量子論の開拓を積極的に進めていったボーアたちの推進派、という構図が思い浮かびます。
付記
「量子論を楽しむ本」の第3章“見ようとすると見えない波”と聞いて思い出したのは、壺と顔の絵です。調べてみるとそれは『ルビンの壺』と呼ばれていました。「壺に集中すると顔に気づかず、顔に集中すると壺に気づかない」というものです。もちろん、これは量子論の“波の収縮”とは全く無関係ですが、ちょっと面白いのでアップしました。

画像出典:「集客コンサルタント橋本慶一のブログ!」









![[原始の大きさ]野球のボール:原子≒地球:ビー玉](https://image.jimcdn.com/app/cms/image/transf/dimension=388x1024:format=jpg/path/s5e68ecbdde7ed919/image/i93f9cd6ab6393083/version/1619304130/image.jpg)